NCERT Solutions for Class 10 Maths Chapter 11 Constructions
In this chapter, you will be dealing with geometric construction problems. NCERT solutions for Class 10 Maths chapter 11 Constructions provide a step-by-step explanation for each problem in the practise exercises. Construction Class 10 Maths chapter 11 NCERT solutions will be useful for homework and board exam preparation. NCERT solutions for Class 10 Maths Chapter 11 are intended to reduce time spent searching for solutions. NCERT solutions for Construction class 10 maths chapter are a valuable resource for enhancing your preparation. NCERT solutions for science and math from classes 6 to 12 are available here. NCERT solutions for class 10 are also available here. Read on to learn more about NCERT solutions Class 10 maths chapter 11 pdf download and other details.
NCERT Solutions for Class 10 Maths Chapter 11 Constructions Excercise: 11.1
In each of the following, give the justification of the construction also:
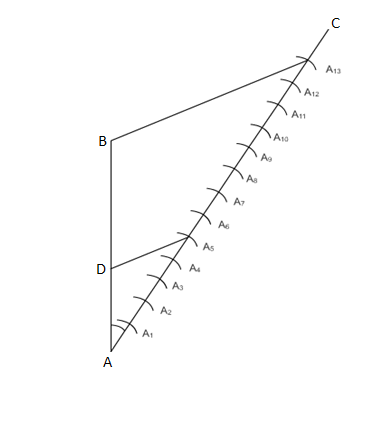
Q1 Draw a line segment of length 7.6 cm and divide it in the ratio 5 : 8. Measure the two parts.
Answer:
Steps of construction:-
(i) Draw a line segment AB of measurement 7.6 cm (length).
(ii) Now draw an acute angle AC with line segment AB.
(iii) Now cut 13 equal points on the line AC where the zeroth point is A.
(iv) Join the 13th point with point B. So the new line is BA 13 .
(v) Now, from point A 5 draw a line parallel to BA 13 on line AB. Name the point as D.
The point D is the required point which divides the line segment in the ratio of 5: 8.
The length of the two parts obtained is 2.9 cm and 4.7 cm for AD and DB respectively.
Justification:- In the figure, we can see two similar triangles: 

Thus .
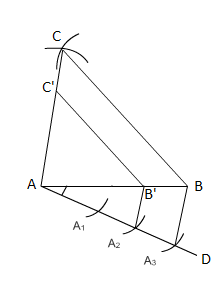
Q2 Construct a triangle of sides 4 cm, 5 cm and 6 cm and then a triangle similar to it whose sides are 2/3 of the corresponding sides of the first triangle.
Answer:
Steps of construction are:-
(i) Firstly draw a line segment AB of length 4 cm.
(ii) Now cut an arc of radius 5 cm from point A and an arc of 6 cm from point B.
(iii) Name the point of intersection of arcs to be point C.
(iv) Now join point AC and BC. Thus 
(v) Draw a line AD which makes an acute angle with AB and is opposite of vertex C.
(vi) Cut three equal parts of line AD namely AA 1 , AA 2 , AA 3 .
(vii) Now join A 3 to B. Draw a line A 2 B’ parallel to A 3 B.
(viii) And then draw a line B’C’ parallel to BC.
Hence 


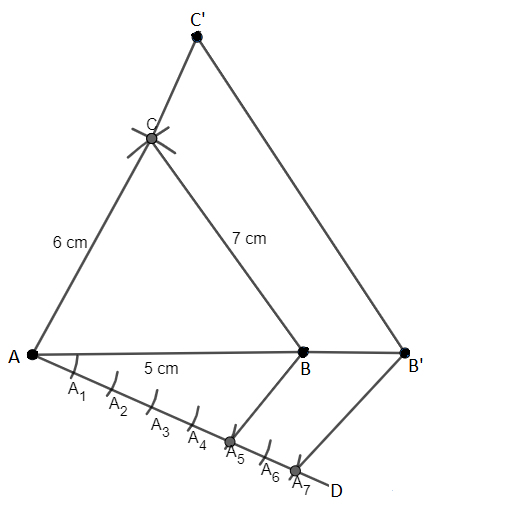
Q3 Construct a triangle with sides 5 cm, 6 cm, and 7 cm and then another triangle whose sides are 7 / 5 of the corresponding sides of the first triangle.
Answer:
Steps of construction are:-
(i) Firstly draw a line segment AB of length 5 cm.
(ii) Now cut an arc of radius 6 cm from point A and an arc of 7 cm from point B.
(iii) Name the point of intersection of arcs to be point C.
(iv) Now join point AC and BC. Thus 
(v) Draw a line AD which makes an acute angle with AB and is opposite of vertex C.
(vi) Cut seven equal parts of line AD namely AA 1 , AA 2 , AA 3 , AA 4 , AA 5 , AA 6 , AA 7 ,.
(vii) Now join A 5 to B. Draw a line A 7 B’ parallel to A 5 B.
(viii) And then draw a line B’C’ parallel to BC.
Hence 


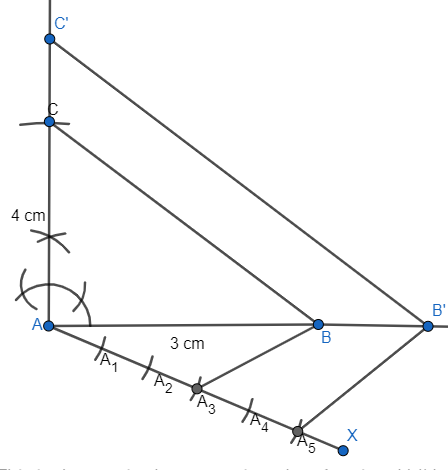
Q4 Construct an isosceles triangle whose base is 8 cm and altitude 4 cm and then another triangle whose sides are 3/ 2 times the corresponding sides of the isosceles triangle.
Answer:
Steps of construction:-
(i) Draw a line segment AB of length 8 cm.
(ii) Cut arcs taking point A and point B as the center. Draw the line to intersect on line segment AB. Mark the intersecting point as point D.
(iii) Cut arc of length 4 cm on the same line which will be the altitude of the triangle.
(iv) Name the point as C. Then 
(v) Draw a line AX which makes an acute angle with AB and is opposite of vertex C.
(vi) Cut seven equal parts of line AX namely AA 1 , AA 2 , AA 3 .
(vii) Now join A 2 to B. Draw a line A 3 B’ parallel to A 2 B.
(viii) And then draw a line B’C’ parallel to BC.
Hence 
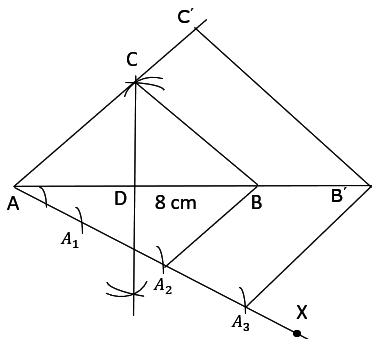


Q5 Draw a triangle ABC with side BC = 6 cm, AB = 5 cm and ABC = 60°. Then construct a triangle whose sides are 3/4 of the corresponding sides of the triangle ABC.
Answer:
Steps of construction:-
(i) Draw a line segment BC with a measurement of 6 cm.
(ii) Now construct angle 60 o from point B and draw AB = 5 cm.
(iii) Join point C with point A. Thus 
(iv) Draw a line BX which makes an acute angle with BC and is opposite of vertex A.
(v) Cut four equal parts of line BX namely BB 1 , BB 2 , BB 3 , BB 4.
(vi) Now join B 4 to C. Draw a line B 3 C’ parallel to B 4 C.
(vii) And then draw a line B’C’ parallel to BC.
Hence 
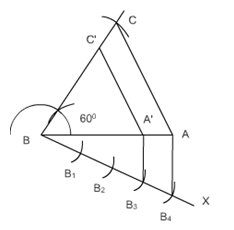


Q6 Draw a triangle ABC with side BC = 7 cm, B = 45°, A = 105°. Then, construct a triangle whose sides are 4/3 times the corresponding sides of D ABC.
Answer:
Steps of construction:-
(i) Draw a line segment BC.
(ii) Now draw an angle 

(iii) Name the intersection of these lines as A.
(iv) Thus 
(v) Draw a line BX which makes an acute angle with BC and is opposite of vertex A.
(vi) Cut four equal parts of line BX namely BB 1 , BB 2 , BB 3 , BB 4.
(vii) Now join B 3 to C. Draw a line B 4 C’ parallel to B 3 C.
(viii) And then draw a line B’C’ parallel to BC.
Hence 
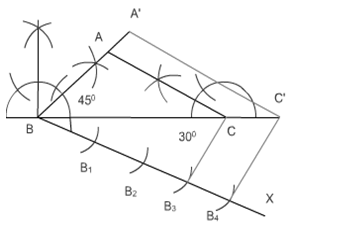


Q7 Draw a right triangle in which the sides (other than hypotenuse) are of lengths 4 cm and 3 cm. Then construct another triangle whose sides are 5/3 times the corresponding sides of the given triangle.
Answer:
Steps of construction:-
(i) Draw a line segment AB having a length of 4 cm.
(ii) Now, construct a right angle at point A and make a line of 3 cm.
(iii) Name this point C. Thus 
(iv) Draw a line AX which makes an acute angle with AB and is opposite of vertex C.
(v) Cut four equal parts of line AX namely AA 1 , AA 2 , AA 3 , AA 4 , AA 5 .
(vi) Now join A 3 to B. Draw a line A 5 B’ parallel to A 3 B.
(vii) And then draw a line B’C’ parallel to BC.
Hence 


NCERT Solutions for Class 10 Maths Chapter 11 Constructions Excercise: 11.2
Q1 In each of the following, give also the justification of the construction:
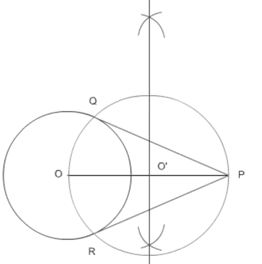
Draw a circle of radius 6 cm. From a point 10 cm away from its center, construct the pair of tangents to the circle and measure their lengths.
Answer:
Steps of construction:-
(i) Taking point O as center draw a circle of radius 6 cm.
(ii) Now, name a point P which is 10 cm away from point O. Join OP.
(iii) Draw a perpendicular bisector of OP name the intersection point of bisector and OP as O’.
(iv) Now draw a circle considering O’ as center and O’P as the radius.
(v) Name the intersection point of circles as Q and R.
(vi) Join PQ and PR. These are the required tangents.
(vii) Measure lengths of PQ = 8cm and PR = 8cm


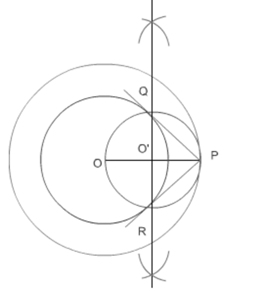
Q2 Construct a tangent to a circle of radius 4 cm from a point on the concentric circle of radius 6 cm and measure its length. Also, verify the measurement by actual calculation.
Answer:
Steps of constructions:-
(i) Taking point O as a center draw a circle of radius 4 cm.
(ii) Now taking O as center draw a concentric circle of radius 6 cm.
(iii) Taking any point P on the outer circle, join OP.
(iv) Draw a perpendicular bisector of OP.
(v) Name the intersection of bisector and OP as O’.
(vi) Now, draw a circle taking O’ as center and O’P as the radius.
(vii) Name the intersection point of two circles as R and Q.
(viii) Join PR and PQ. These are the required tangents.
(ix) Measure the lengths of the tangents. PR = 4.47 cm and PQ = 4.47 cm.


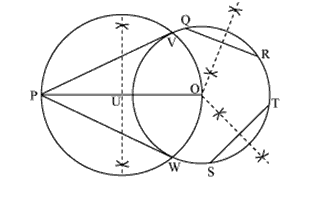
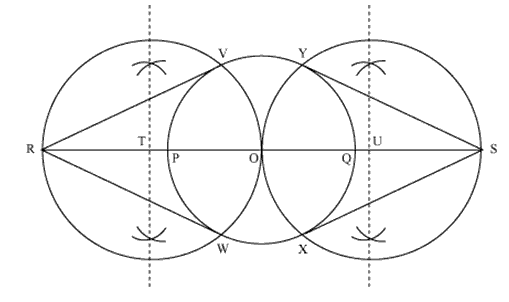
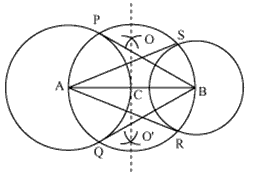
Q3 Draw a circle of radius 3 cm. Take two points P and Q on one of its extended diameter each at a distance of 7 cm from its center. Draw tangents to the circle from these two points P and Q.
Answer:
Steps of construction:-
(i) Taking O as a center draw a circle of radius 3 cm.
(ii) Now draw a diameter PQ of this circle and extend it.
(iii) Mark two points R and S on the extended diameter such that OR = OS = 7 cm.
(iv) Draw the perpendicular bisector of both the lines and name their mid-points as T and U.
(v) Now, taking T and U as center draw circles of radius TR and QS.
(vi) Name the intersecting points of the circles with the first circles as V, W, X, Y.
(vii) Join the lines. These are the required tangents.


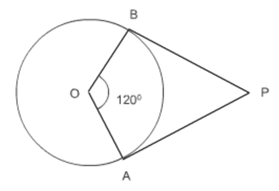
Q4 Draw a pair of tangents to a circle of radius 5 cm which is inclined to each other at an angle of 60°.
Answer:
Steps of construction:-
(i) Draw a circle with center O and radius 5 cm.
(ii) Now mark a point A on the circumference of the circle. And draw a line AP perpendicular to the radius OA.
(iii) Mark a point B on the circumference of the circle such that 
(iv) Join B to point P.
(v) AP and BP are the required tangents.


Q5 Draw a line segment AB of length 8 cm. Taking A as a center, draw a circle of radius 4 cm and taking B as center, draw another circle of radius 3 cm. Construct tangents to each circle from the center of the other circle.
Answer:
Steps of construction:-
(i) Draw a line segment AB having a length of 8 cm.
(ii) Now, taking A as a center draw a circle of radius 4 cm. And taking B as a center draw a circle of radius 3 cm.
(iii) Bisect the line AB and name the mid-point as C.
(iv) Taking C as a center and AC as radius draw a circle.
(v) Name the intersection points of the circle as P, Q, R, S.
(vi) Join the lines and these are our required tangents.


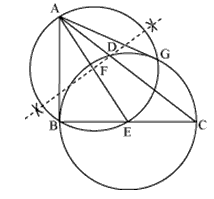
Q6 Let ABC be a right triangle in which AB = 6 cm, BC = 8 cm and B = . BD is perpendicular from B on AC. The circle through B, C, D is drawn. Construct the tangents from A to this circle.
Answer:
Steps of construction:-
(i) Draw a line segment BC of length 8 cm.
(ii) Construct a right angle at point B. Now draw a line of length 6 cm. Name the other point as A.
(iii) Join AC. 
(iv) Now construct a line BD on the line segment AC such that BD is perpendicular to AC.
(v) Now draw a circle taking E as a center (E is the midpoint of line BC) and BE as the radius.
(vi) Join AE. And draw a perpendicular bisector of this line.
(vii) Name the midpoint of AE as F.
(viii) Now, draw a circle with F as center and AF as the radius.
(ix) Name the intersection point of both the circles as G.
(x) Join AG. Thus AB and AG are the required tangents.


Q7 Draw a circle with the help of a bangle. Take a point outside the circle. Construct the pair of tangents from this point to the circle.
Answer:
Steps of construction:-
(i) Draw a circle using a bangle.
(ii) Now draw 2 chords of this circle as QR and ST.
(iii) Take a point P outside the circle.
(iv) Draw perpendicular bisector of both the chords and let them meet at point O.
(v) Joinpoint PO.
(vi) Draw bisector of PO and name the midpoint as U.
(vii) Now, taking U as a center and UP as radius draw a circle.
(viii) Name the intersection point of both the circles as V and W.
(ix) Join PV and PW. These are the required tangents.