NCERT Solutions for Class 10 Maths Chapter 10 Circles
To better understand the chapters, students should consult the NCERT Class 10 Maths solutions chapter 10. NCERT Solutions for Class 10 Maths Chapter 10 Circles introduces some difficult and important concepts such as tangents, tangents to a circle, and the number of tangents from a point on a circle. Students will learn about the various conditions that arise when a line and a circle are given in a plane in the Circles Class 10 chapter. NCERT solutions for Science and Math for Classes 6 to 12 are available here. NCERT Solutions for Class 10 Maths Chapter 10 Circles will assist students in planning their exam preparation. It is best to finish the NCERT Class 10 Maths syllabus as soon as possible. For exam preparation, students should also consult the NCERT Class 10 Maths books.
NCERT solutions for Class 10 Maths chapter 10 Circles Excercise: 10.1
Q1 How many tangents can a circle have?
Answer:
The lines that intersect the circle exactly at one single point are called tangents. In a circle, there can be infinitely many tangents.
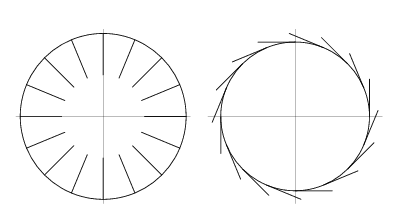



Q2 Fill in the blanks :
(1) A tangent to a circle intersects it in_________ point (s).
(2) A line intersecting a circle in two points is called a _____.
(3) A circle can have ________ parallel tangents at the most.
(4) The common point of a tangent to a circle and the circle ______
Answer:
(a) one
A tangent of a circle intersects the circle exactly in one single point.
(b) secant
It is a line that intersects the circle at two points.
(c) Two,
There can be only two parallel tangents to a circle.
(d) point of contact
The common point of a tangent and a circle.
Q3 A tangent PQ at a point P of a circle of radius 5 cm meets a line through the center O at a point Q so that OQ = 12 cm. Length PQ is :
(A) 12 cm
(B) 13 cm
(C) 8.5 cm
(D) 
Answer:
The correct option is (d) = 
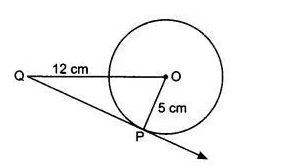


![]()
![]()
![]()
It is given that the radius of the circle is 5 cm. OQ = 12 cm
According to question,
We know that 
So, triangle OPQ is a right-angle triangle. By using Pythagoras theorem,

Q4 Draw a circle and two lines parallel to a given line such that one is a tangent and the other, a secant to the circle.
Answer:
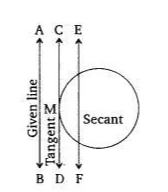


![]()
![]()
![]()
AB is the given line and the line CD is the tangent to a circle at point M and parallels to the line AB. The line EF is a secant parallel to the AB
NCERT solutions for class 10 maths chapter 10 Circles Excercise: 10.2
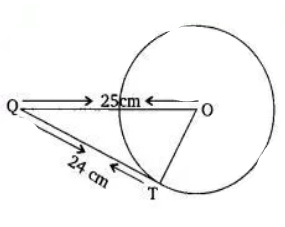
Q1 From a point Q, the length of the tangent to a circle is 24 cm and the distance of Q from the center is 25 cm. The radius of the circle is
(A) 7 cm
(B) 12 cm
(C) 15 cm
(D) 24.5 cm
Answer:
The correct option is (A) = 7 cm
Given that,
The length of the tangent (QT) is 24 cm and the length of OQ is 25 cm.
Suppose the length of the radius OT be 
We know that 



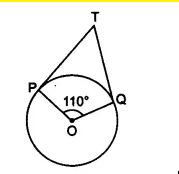
Q2 In Fig. 10.11, if TP and TQ are the two tangents to a circle with center O so that POQ = , then PTQ is equal to
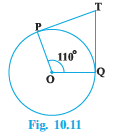


(A) 
(B) 
(C) 
(D) 
Answer:
The correct option is (b)


![]()
![]()
![]()
In figure, 
Since POQT is quadrilateral. Therefore the sum of the opposite angles are 180



Q3 If tangents PA and PB from a point P to a circle with center O are inclined to each other at an angle of , then POA is equal to
(A) 50°
(B) 60°
(C) 70°
(D) 80°
Answer:
The correct option is (A)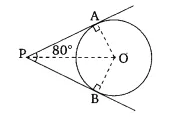


![]()
![]()
![]()
It is given that, tangent PA and PB from point P inclined at 
In triangle 


OA =OB (radii of the circle)
PA = PB (tangents of the circle)
Therefore, by SAS congruence
By CPCT, 
Now, 
In 


= 50
Q4 Prove that the tangents drawn at the ends of a diameter of a circle are parallel.
Answer:
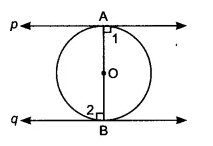


![]()
![]()
![]()
Let line 

OA and OB are perpendicular to the tangents 

therefore,






Q5 Prove that the perpendicular at the point of contact to the tangent to a circle passes through the center.
Answer:
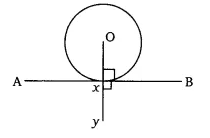


![]()
![]()
![]()
In the above figure, the line AXB is the tangent to a circle with center O. Here, OX is the perpendicular to the tangent AXB ( 
Therefore, we have,




Q6 The length of a tangent from a point A at distance 5 cm from the center of the circle is 4 cm. Find the radius of the circle.
Answer:
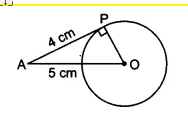


![]()
![]()
![]()
Given that,
the length of the tangent from the point A (AP) is 4 cm and the length of OA is 5 cm.
Since 
Therefore, 




Q7 Two concentric circles are of radii 5 cm and 3 cm. Find the length of the chord of the larger circle which touches the smaller circle.
Answer:
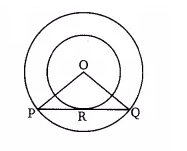


![]()
![]()
![]()
In the above figure, Pq is the chord to the larger circle, which is also tangent to a smaller circle at the point of contact R.
We have,
radius of the larger circle OP = OQ = 5 cm
radius of the small circle (OR) = 3 cm
OR 
According to question,
In 




OR = OR {common}
OP = OQ {both radii}
By RHS congruence 


So, by CPCT
PR = RQ
Now, In 
by using pythagoras theorem,
PR = 4 cm
Hence, PQ = 2.PR = 8 cm
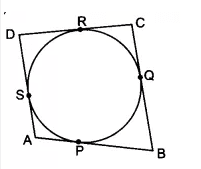
Q8 A quadrilateral ABCD is drawn to circumscribe a circle (see Fig. 10.12). Prove that AB + CD = AD + BC
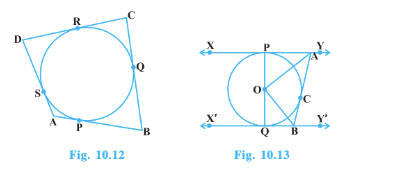





Answer:


![]()
![]()
![]()
To prove- AB + CD = AD + BC
Proof-
We have,
Since the length of the tangents drawn from an external point to a circle are equal
AP =AS …….(i)
BP = BQ………(ii)
AS = AP………..(iii)
CR = CQ ………..(iv)
By adding all the equations, we get;
AP + BP +RD+ CR = AS +DS +BQ +CQ

Hence proved.
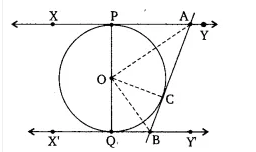
Q9 In Fig. 10.13, XY and X’Y’are two parallel tangents to a circle with center O and another tangent AB with a point of contact C intersecting XY at A and X’Y’ at B. Prove that AOB = 90°.
Answer:


![]()
![]()
![]()
To prove- 

Proof-
In 

OA =OA [Common]
OP = OC [Both radii]
AP =AC [tangents from external point A]
Therefore by SSS congruence, 


and by CPCT, 


Similarly, from 



Adding eq (1) and eq (2)


2( 

( 

Now, in 
Sum of interior angle is 180.
So, 




hence proved.
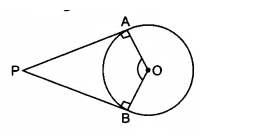
Q10 Prove that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtended by the line-segment joining the points of contact at the center.
Answer:


![]()
![]()
![]()
To prove – 
Proof-
We have, PA and PB are two tangents, B and A are the point of contacts of the tangent to a circle. And 

According to question,
In quadrilateral PAOB,




90 + 


Hence proved .
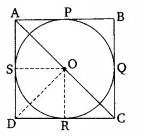
Q11 Prove that the parallelogram circumscribing a circle is a rhombus.
Answer:


![]()
![]()
![]()
To prove – the parallelogram circumscribing a circle is a rhombus
Proof-
ABCD is a parallelogram that circumscribes a circle with center O.
P, Q, R, S are the points of contacts on sides AB, BC, CD, and DA respectively
AB = CD .and AD = BC………..(i)
It is known that tangents drawn from an external point are equal in length.
RD = DS ………..(ii)
RC = QC………..(iii)
BP = BQ………..(iv)
AP = AS ………….(v)
By adding eq (ii) to eq (v) we get;
(RD + RC) + (BP + AP) = (DS + AS) + (BQ + QC)
CD + AB = AD + BC

Now, AB = AD and AB = CD
Hence ABCD is a rhombus.
Q12 A triangle ABC is drawn to circumscribe a circle of radius 4 cm such that the segments BD and DC into which BC is divided by the point of contact D are of lengths 8 cm and 6 cm respectively (see Fig. 10.14). Find the sides AB and AC.
Answer:
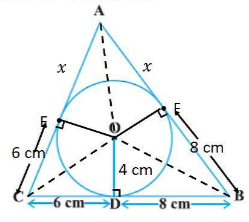


Consider the above figure. Assume center O touches the sides AB and AC of the triangle at point E and F respectively.
Let the length of AE is x.
Now in 



Now AB = AE + EB

Now s = (x + 8 + 14 + 6 +x)/2\\\\ => s = (2x + 28)/2\\\\ => s = x + 14″ src=”https://entrancecorner.codecogs.com/gif.latex?%5C%5Cs%20%3D%20%28AB%20+%20BC%20+%20CA%20%29/2%5C%5C%5C%5C%20%3D%3E%20s%20%3D%20%28x%20+%208%20+%2014%20+%206%20+x%29/2%5C%5C%5C%5C%20%3D%3E%20s%20%3D%20%282x%20+%2028%29/2%5C%5C%5C%5C%20%3D%3E%20s%20%3D%20x%20+%2014″>
Area of triangle 
![\\=\sqrt{s*(s-a)*(s-b)*(s-c)}\\\\=\sqrt{(14+x)*[(14+x)-14]*[(14+x)-(6+x)]*[(14+x)-(8+x)]}\\\\=4\sqrt{3(14x+x^2)}](http://careerssutra.com/wp-content/plugins/a3-lazy-load/assets/images/lazy_placeholder.gif)
Now the area of 

Area of 

Area of 

Now Area of the 



![\\=> 4\sqrt{3x(14+x)}= 28 + 12 + 2x + 16 + 2x \\\\=> 4\sqrt{3x(14+x)} = 56 + 4x \\\\=> 4\sqrt{3x(14+x)} = 4(14 + x) \\\\=> \sqrt{3x(14+x)}] = 14 + x](http://careerssutra.com/wp-content/plugins/a3-lazy-load/assets/images/lazy_placeholder.gif)
On squaring both the side, we get

Hence
AB = x + 8
=> AB = 7+8
=> AB = 15
AC = 6 + x
=> AC = 6 + 7
=> AC = 13
Answer- AB = 15 and AC = 13
Q13 Prove that opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the center of the circle.
Answer:
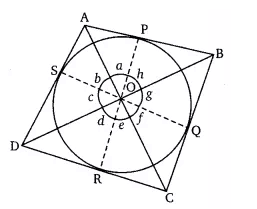


![]()
![]()
![]()
Given- ABCD is a quadrilateral circumscribing a circle. P, Q, R, S are the point of contact on sides AB, BC, CD, and DA respectively.
To prove-
Proof –
Join OP, OQ, OR and OS
In triangle 

OD =OD [common]
OS = OR [radii of same circle]
DR = DS [length of tangents drawn from an external point are equal ]
By SSS congruency, 


and by CPCT, 


Similarily,


SImilarily, 
Hence proved.