NCERT Solutions for Class 10 Maths Chapter 12 Areas Related to Circles
Circle-Related Area The Class 10 chapter builds on the Class 9 chapter ‘Circles,’ which you have already completed. There are many questions in NCERT Chapter 12 Maths Class 10 that use Class 9 concepts. There are three exercises with 35 questions in NCERT Class 10 Maths book chapter 12. The NCERT solutions for Class 10 Maths chapter 12 Areas Related to Circles include the correct answer as well as solutions to all of the questions.
NCERT Solutions for Class 10 Maths Chapter 12 Areas Related to Circles Excercise: 12.1
Q1 The radii of two circles are 19 cm and 9 cm respectively. Find the radius of the circle which has a circumference equal to the sum of the circumferences of the two circles.
Answer:
Circumference of 1st circle is given :

And the circumference of the 2nd circle is: 
Thus the circumference of the new circle is 
or 
or 
Hence the radius of the new circle is 28 cm.
Q2 The radii of two circles are 8 cm and 6 cm respectively. Find the radius of the circle having an area equal to the sum of the areas of the two circles.
Answer:
We know that the area of the circle is: 
Thus area of a 1st circle: 
or 
And the area of a 2nd circle is : 
or 
According to the question area of the new circle is 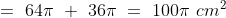
or 
or 
Hence the area of the new circle is 10 cm.
Q3 Fig. depicts an archery target marked with its five scoring regions from the center outwards as Gold, Red, Blue, Black, and White. The diameter of the region representing the Gold score is 21 cm and each of the other bands is 10.5 cm wide. Find the area of each of the five scoring regions.



Answer:
The radius of each scoring region can be found by adding 10.5 in respective colors.
The area of the golden region is: 
Similarly area of the red region is = Area of a red score – Area of the golden region

Then the area of the blue region is:

And the area of the black region is:

Area of the white region is:

Q4 The wheels of a car are of diameter 80 cm each. How many complete revolutions does each wheel make in 10 minutes when the car is traveling at a speed of 66 km per hour?
Answer:
Let the number of revolution of the wheel be n.
The circumference of the wheel is given by :-

Now, the speed of the car is given by :-

Thus distance traveled in 10 minutes is: 
According to the question, we get;

or 
Hence the number of revolutions made by the wheel is 4372.
Q5 Tick the correct answer in the following and justify your choice : If the perimeter and the area of a circle are numerically equal, then the radius of the circle is
(A) 2 units
(B) 
(C) 4 units
(D) 7 units
Answer:
Let the radius of the circle be r.
Then according to question, we can write:-
Perimeter = Area

Hence option (A) is correct.
NCERT Solutions for Class 10 Maths Chapter 12 Areas Related to Circles Excercise: 12.2
Q1 Find the area of a sector of a circle with radius 6 cm if angle of the sector is 60°.
Answer:
We know that the area of a sector having radius r and angle 

Thus the area of the given sector is:-

Q2 Find the area of a quadrant of a circle whose circumference is 22 cm.
Answer:
We are given the circumference of the circle.
Thus,

Also, we know that the area of a sector is given by :

It is given that we need to find the area of a quadrant thus 
Hence the area becomes:-

Q3 The length of the minute hand of a clock is 14 cm. Find the area swept by the minute hand in 5 minutes.
Answer:
The minute hand rotates 360 o in one hour.
We need to find rotation in 5 min. :-

The area of the sector is given by :

Hence the area swept by minute hand in 5 minutes is.
Q4 A chord of a circle of radius 10 cm subtends a right angle at the center. Find the area of the corresponding : (i) minor segment
Answer:
The angle in the minor sector is 90 o.
Thus the area of the sector is given by :-

Now the area of a triangle is :-

Thus the area of minor segment = Area of the sector – Area of a triangle
or 
Q4 A chord of a circle of radius 10 cm subtends a right angle at the center. Find the area of the corresponding : (ii) major sector. (Use π = 3.14)
Answer:
The area of the major sector can be found directly by using the formula:

In the case of this, the angle is 360 o – 90 o = 270 o.
Thus the area is : –

Q5 In a circle of radius 21 cm, an arc subtends an angle of 60° at the center. Find: (i) the length of the arc
Answer:
The length of the arc is given by :-


Hence the length of the arc is 22 cm.
Q5 In a circle of radius 21 cm, an arc subtends an angle of 60° at the center. Find: (ii) area of the sector formed by the arc.
Answer:
We know that the area of the sector is given by:-


Thus the area of the sector is 231 cm 2.
Q5 In a circle of radius 21 cm, an arc subtends an angle of 60° at the center. Find: (iii) area of the segment formed by the corresponding chord
Answer:
For the area of the segment, we need to subtract the area of the triangle attached with the area of arc.
Thus consider the triangle :-
It is given that the angle of arc is 60 o , or we can say that all angles are 60 o (since two sides are equal). Hence it is an equilateral triangle.
Area of triangle is :-

Hence the area of segment is :-

Q6 A chord of a circle of radius 15 cm subtends an angle of 60° at the center. Find the areas of the corresponding minor and major segments of the circle.
(Use and )
Answer:
The area of the sector is :

Now consider the triangle, the angle of the sector is 60 0.
This implies it is an equilateral triangle. (As two sides are equal so will have the same angle. This possible only when all angles are equal i.e., 60 o .)
Thus, the area of the triangle is:-

or 
Hence area of the minor segment: 
And the area of the major segment is :

or 
or 
or 
Q7 A chord of a circle of radius 12 cm subtends an angle of 120° at the center. Find the area of the corresponding segment of the circle.
(Use and )
Answer:
For the area of the segment, we need the area of sector and area of the associated triangle.
So, the area of the sector is:

or 
Now, consider the triangle :-
Draw a perpendicular from the center of the circle on the base of the triangle (let it be h).
Using geometry we can write,

or 
Similarly, 
or 
Thus the area of the triangle is:

or 
Hence the area of segment is: 
Q8 A horse is tied to a peg at one corner of a square shaped grass field of side 15 m by means of a 5 m long rope (see Fig.). Find (i) the area of that part of the field in which the horse can graze.


Answer:
The part grazed by the horse is given by = Area of sector



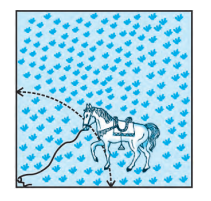
Q8 A horse is tied to a peg at one corner of a square shaped grass field of side 15 m by means of a 5 m long rope (see Fig.). Find (ii) the increase in the grazing area if the rope were 10 m long instead of 5 m. (Use )


Answer:
When the length of the rope is 10 m, the area grazed will be:-



Hence the change in the grazing area is given by :

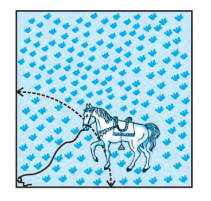
Q9 A brooch is made with silver wire in the form of a circle with a diameter of 35 mm. The wire is also used in making 5 diameters which divide the circle into 10 equal sectors as shown in Fig. Find: (i) the total length of the silver wire required.


Answer:
The total wire required will be for 5 diameters and the circumference of the brooch.
The circumference of the brooch :-

Hence the total wire required will be:- .
Q9 A brooch is made with silver wire in the form of a circle with a diameter of 35 mm. The wire is also used in making 5 diameters which divide the circle into 10 equal sectors as shown in Fig. 12.12. Find : (ii) the area of each sector of the brooch.
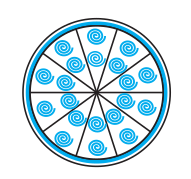


Answer:
The total number of lines present in the brooch is 10 (line starting from the centre).
Thus the angle of each sector is 36 o .
The area of the sector is given by:-

Q10 An umbrella has 8 ribs that are equally spaced (see Fig. ). Assuming umbrella to be a flat circle of radius 45 cm, find the area between the two consecutive ribs of the umbrella.
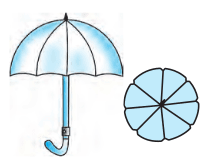


Answer:
It is given that the umbrella has 8 ribs so the angle of each sector is 45 o.
Thus the area of the sector is given by :-

Hence the area between two consecutive ribs is.
Q11 A car has two wipers that do not overlap. Each wiper has a blade of length 25 cm sweeping through an angle of 115°. Find the total area cleaned at each sweep of the blades.
Answer:
The area cleaned by one wiper is :-

or 
or 
Hence the required area (area cleaned by both blades) is given by :-

Q12 To warn ships for underwater rocks, a lighthouse spreads a red-colored light over a sector of angle 80° to a distance of 16.5 km. Find the area of the sea over which the ships are warned. (Use π = 3.14)
Answer:
The area of the sector is given by :-

In this case, the angle is 80 o.
Thus the area is :-

or 
Q13 A round table cover has six equal designs as shown in Fig. If the radius of the cover is 28 cm, find the cost of making the designs at the rate of Rs. 0.35 per cm 2. (Use )
Answer:
The angle of each of the six sectors is 60 o at the center. 
Area of the sector is given by :-

or 
or 
And the area of the equilateral triangle associated with segment :-

or 
Hence the area of segment is: 
Thus the total area of design is: 
So, the total cost for the design is :- 
Q14 Tick the correct answer in the following:
Area of a sector of angle p (in degrees) of a circle with radius R is
(A) 
(B) 
(C) 
(D) 
Answer:
We know that the area of the sector is given by :-


Hence option (d) is correct.
NCERT Solutions for Class 10 Maths Chapter 12 Areas Related to Circles Excercise: 12.3
Q1 Find the area of the shaded region in Fig, if PQ = 24 cm, PR = 7 cm, and O is the center of the circle.
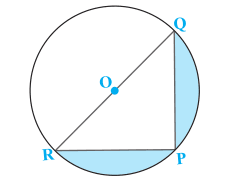


Answer:
We know that 
RQ can be found using the Pythagoras theorem.

or 
or 
Now, the area of the shaded region is given by = Area of semicircle – Area of 
Area of a semicircle is:-

or 
or 
And, the area of triangle PQR is:

Hence the area of the shaded region is:
Q2 Find the area of the shaded region in Fig, if radii of the two concentric circles with centre O are 7 cm and 14 cm respectively and.
Answer:
The area of a shaded region can be easily found by using the formula of the area of the sector.
Area of the shaded region is given by : Area of sector OAFC – Area of sector OBED



Q3 Find the area of the shaded region in Fig, if ABCD is a square of side 14 cm and APD and BPC are semicircles. 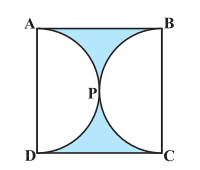


Answer:
Area of the shaded region is given by = Area of the square – Area of two semicircles.
Area of square is : 
And the area of the semicircle is :-



Hence the area of the shaded region is given by:
Q4 Find the area of the shaded region in Fig, where a circular arc of radius 6 cm has been drawn with vertex O of an equilateral triangle OAB of side 12 cm as the centre. 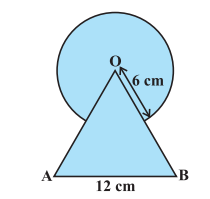


Answer:
Area of the shaded region is given by = Area of triangle + Area of the circle – Area of the sector
Area of the sector is : –

or 
And, the area of the triangle is:

And, the area of the circle is: 
or 
or 
Hence the area of the shaded region is :-

or 
Q5 From each corner of a square of side 4 cm a quadrant of a circle of radius 1 cm is cut and also a circle of diameter 2 cm is cut as shown in Fig. Find the area of the remaining portion of the square. 
Answer:
Consider the quadrant in the given figure:- We have an angle of the sector as 90 o and radius 1 cm.
Thus the area of the quadrant is :-

or 
And the area of the square is : 


And, the area of the circle is:-

Hence the area of the shaded region is: = Area of the square – Area of the circle – 4 (Area of quadrant)
or 
or 
Q6 In a circular table cover of radius 32 cm, a design is formed leaving an equilateral triangle ABC in the middle as shown in Fig. Find the area of the design.
Answer:
Assume the center of the circle to be point C and AD as the median of the equilateral triangle.
Then we can write:-

or 
Thus 
Consider 

or 
or 
Thus the area of an equilateral triangle is:-

or 
And the area of the circle is : 
or 
Hence the area of the design is:-

Q7. In Fig, ABCD is a square of side 14 cm. With centers A, B, C, and D, four circles are drawn such that each circle touch externally two of the remaining three circles. Find the area of the shaded region.
Answer:
It is clear from the figure that the area of all sectors is equal (due to symmetry).
Also, the angle of the sector is 90 o and the radius is 7 cm.
Thus the area of the sector is:-

or 
And, the area of the square is : 
Hence the area of the shaded region is :


Q8 Fig. depicts a racing track whose left and right ends are semicircular.
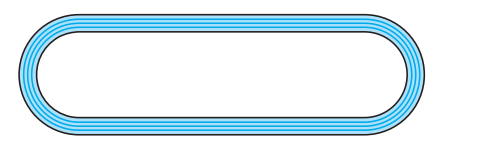


The distance between the two inner parallel line segments is 60 m and they are each 106 m long. If the track is 10 m wide, find :
(i) the distance around the track along its inner edge
Answer:
The distance around the track is Length of two straight lines + Length of two arcs.
Length of the arc is –


Thus the length of the inner track is :



Q8 Fig. depicts a racing track whose left and right ends are semicircular.
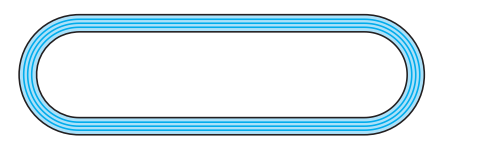


The distance between the two inner parallel line segments is 60 m and they are each 106 m long. If the track is 10 m wide, find :
(ii) the area of the track.
Answer:
The area of track = Area of outer structure – Area of inner structure.
Area of outer structure is: = Area of square + Area of 2 semicircles

And, area of inner structure: = Area of inner square + Area of 2 inner semicircles

Thus the area of the track is :

Hence the area of the track is 4320 m 2 .
Q9 In Fig, AB, and CD are two diameters of a circle (with center O) perpendicular to each other and OD is the diameter of the smaller circle. If OA = 7 cm, find the area of the shaded region.
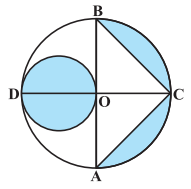


Answer:
Firstly, the area of the smaller circle is :



Now, the area of 

or 
And, the area of the bigger semicircle is :



Hence the area of the shaded region is:-


Therefore the area of the shaded region is 66.5 cm 2 .
Q10 The area of an equilateral triangle ABC is 17320.5 cm 2 . With each vertex of the triangle as the centre, a circle is drawn with a radius equal to half the length of the side of the triangle (see Fig.). Find the area of the shaded region. (Use and )
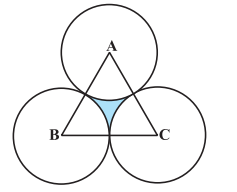


Answer:
Area of an equilateral triangle is:-



Now, consider the sector:- Angle of the sector is 60 o and the radius is 100 cm.
Thus the area of the sector:-


Thus the area of the shaded region is :


Q11 On a square handkerchief, nine circular designs each of radius 7 cm are made (see Fig.). Find the area of the remaining portion of the handkerchief.
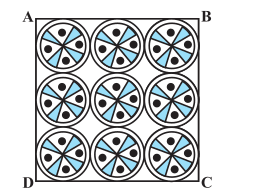


Answer:
Since one side of the square has 3 circles, thus the side of the square is 42 cm.
Area of the square : 
And, area of a circle :


Hence the area of the remaining portion is : 

Q12 In Fig, OACB is a quadrant of a circle with center O and radius 3.5 cm. If OD = 2 cm, find the area of the (i) quadrant OACB
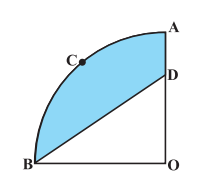


Answer:
The quadrant OACB is a sector with angle 90 o and radius 3.5 cm.
Thus the area of the quadrant is:-


Hence the area of the quadrant is .
Q12 In Fig, OACB is a quadrant of a circle with centre O and radius 3.5 cm. If OD = 2 cm, find the area of the (ii) shaded region.
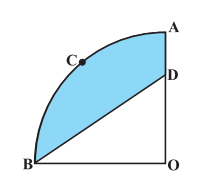


Answer:
For area of shaded region we need to find area of the triangle.
Area of triangle is:-


Hence the area of the shaded region is = Area of the quadrant – Area of triangle


Q13 In Fig, a square OABC is inscribed in a quadrant OPBQ. If OA = 20 cm, find the area of the shaded region. (Use )
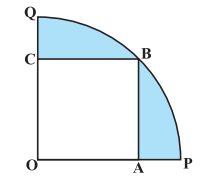


Answer:
In the given figure we need to find the radius of the circle:-
Consider 



Thus area of quadrant:-


Also, the area of the square is : 
Area of the shaded region is : 
Q14 AB and CD are respectively arcs of two concentric circles of radii 21 cm and 7 cm and centre O (see Fig.). If , find the area of the shaded region.
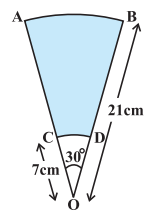


Answer:
Area of the shaded region is = Area of larger sector – Area of smaller sector



Hence the area of the shaded region is 
Q15 In Fig, ABC is a quadrant of a circle of radius 14 cm and a semicircle is drawn with BC as diameter. Find the area of the shaded region.
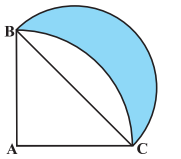


Answer:
Consider 



Area of triangle is :


Now, area of sector is :


And area of semicircle is : –



Hence the area of the shaded region is :
Q16 Calculate the area of the designed region in fig. common between the two quadrants of circles of radius 8 cm each.
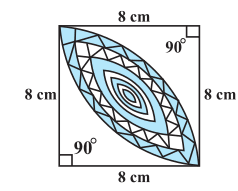


Answer:
It is clear from the figure that the required area (designed area) is the area of the intersection of two sectors.
Area of the sector is:-


And, area of the triangle:-

Hence the area of the designed region is :

